Contents

Summary

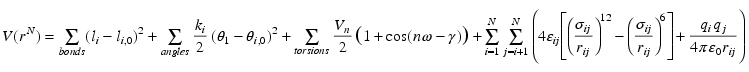
1. A key function of biological membranes is to provide mechanisms for controlled transport of ions, nutrients, metabolites, peptides and proteins between a cell and its environment.

2. We are using computer simulations to study several processes involved in transport.

3. In model membranes, the distribution of small molecules can be accurately calculated; we are making progress toward understanding the factors that determine the partitioning behaviour in the inhomogeneous lipid environment, with implications for, e.g. drug distribution, membrane protein folding, and the energetics of voltage-gating.

4. Lipid bilayers can be simulated at a scale that is sufficiently large to study significant defects such as those caused by electroporation.

5. Computer simulations of complex membrane proteins such as potassium channels and ATP-binding cassette transporters can give detailed information about the atomistic dynamics that forms the basis of ion transport, selectivity, conformational change, and the molecular mechanism of ATP-driven transport.

6. I will illustrate this with recent simulation studies of the voltage-gated potassium channel KvAP and the ABC-transporter BtuCD.

Introduction

Detailed computer simulations of lipids and proteins are a powerful method to study the structure, dynamics and interactions of membrane proteins, peptides, and lipids.^1,2 Increasing sophistication of models for the interactions between atoms, modern software, and increasing computer power are now extending molecular dynamics (MD) simulations beyond small patches of pure lipids on a subnanosecond time scale to a wide range of problems on a timescale of hundreds of nanoseconds and, through special techniques, orders of magnitude beyond that. The rapidly growing number of high-resolution structures of membrane proteins and increased knowledge of the principles of membrane protein structure have enabled computer simulations and modelling to become standard techniques to study membrane proteins in atomic detail. Such methods have been applied to understanding the detailed energetics of ion permeation in ion channels,^3-7 water permeation and proton exclusion in aquaporin,^8-10 the mechanism of lipid-based vesicle fusion,^11,12 the mechanism of electroporation,^13,14 the dynamics of ATP-binding cassette (ABC) transporters¹⁵ and a wide range of other problems involving membrane proteins and lipids.^2,16

In this paper I describe recent results on four problems that are related to transport across biological membranes. My aim is to provide an impression of the type of problems that can be fruitfully studied by computer simulation at this time, illustrated using examples from work in my group. The first example concerns calculating the distribution of small molecules in a lipid bilayer. This distribution is a major determinant of the rate of passive permeation of small molecules through a membrane, and is relevant for a number of other problems. The second example considers the molecular mechanism of electroporation, a common lab technique with potential therapeutic applications that involves major rearrangements of the lipids in a membrane. The third example shows the use of MD simulations to investigate a proposed mechanism of voltage-gating in potassium channels using a crystal structure. I include it here not because it gives interesting insight into voltage-gating, but because it illustrates how computer simulations can be used to test hypothetical mechanisms based on a single crystal structure that may or may not be in a physiologically relevant conformation. The last example concerns the mechanism of ABC transporters. This is a complex problem involving large protein complexes, but several aspects of the full problem can be investigated by computer simulation.

The main method we use and one of the most powerful computational methods to study matter at the level of atoms and molecules is molecular dynamics simulation. In MD, the forces between atoms are described by a simplified empirical potential that tries to mimic the ‘real’ underlying interaction potential. Modern quantum chemistry can reproduce almost exactly this real potential for simple cases involving of the order of tens or a hundred atoms, but is currently too expensive computationally for most of the problems we are interested in, and contains details that are not likely to be essential for these problems. The basic method has been reviewed in detail^17,18 and is also well-described in recent textbooks, e.g. refs. 19,20

An example of a frequently used potential function is shown in Equation 1.

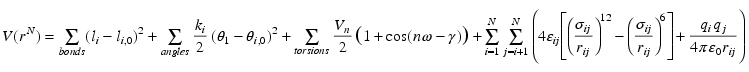
Equation 1.Example potential function.

The primary result of an MD simulation is a trajectory of all atoms in time, from which dynamic, structural and thermodynamic properties of the simulated system can be calculated. The main strength of molecular dynamics simulations is the amount of detail: all or nearly all atoms are incorporated in the model, and few assumptions are necessary. Its main weaknesses are the computational cost and the associated limited time (realistically, at this time, about 100-500 nanoseconds) and limited length scale (ca. 10×10×10nm), and the approximations inherent in the potential function. The use of fixed partial charges centered on the atoms is a particular significant limitation, but there are other areas for improvement, e.g. additional terms that describe coupling between bonded interactions.²¹ There is a substantial ongoing effort to improve the accuracy of the potential functions, but this does not change the fundamental method. An example of a typical membrane simulation is shown in Figure 1.

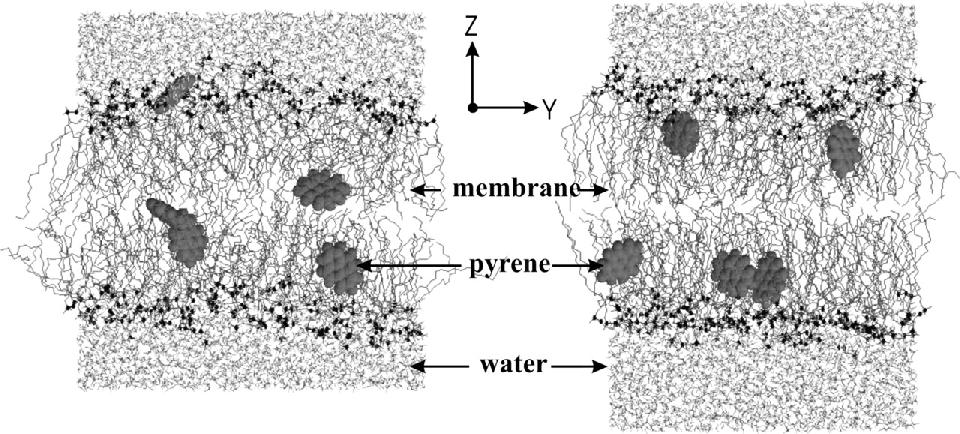
Figure 1. Snapshots of a typical lipid bilayer system, including pyrene molecules. The left snapshot is a starting structure, at the beginning of the simulation. The right snapshot is the structure after 15 ns, showing the equilibrium positions of the pyrene molecules. Reproduced with permission from ref. 31.

Several useful extensions of the basic simulation method make it possible to calculate free energy differences from simulations.²² If a reaction coordinate can be identified for a process, processes that are orders of magnitude slower can be studied than would be possible by direct simulation. Such a reaction coordinate could be a concerted conformational change, or a pathway for ion permeation in ion channels. In umbrella sampling, a biasing potential is used to restrict a simulated system to sample phase space within a specified region (called a window). By placing windows along the reaction coordinate, one can generate a free energy profile (also called potential of mean force), which will quantitatively describe why one region of space is more favourable than another. The distribution of hexane in a lipid bilayer as calculated below is a detailed example. If one would monitor the distribution of hexane throughout the simulation, there would be insufficient statistical information about areas that hexane visits with low probability (e.g. in the lipid head groups and in water, compared to the bilayer interior). By restraining a hexane molecule at different locations in the bilayer – effectively forcing the hexane molecule to spend time in unfavourable regions of the system - a distribution of hexane can be calculated that depends both on the restraining potential and the actual distribution without the restraining potential. From a set of such simulations it is possible to reconstruct the entire distribution by correcting for the restraining potentials. The result is an accurate distribution even for cases where there is a very large difference in free energy between the least and the most favourable positions. Combined with additional calculations, properties such as rates become accessible. An interesting example is permeation in ion channels.²³ A second example is a calculation of the flip-flop rate of lipids, which is measured in hours, from microsecond simulations (Tieleman & Marrink, submitted).

One of the major challenges in modern simulations is the study of conformational changes in proteins that are too slow to observe directly on a time scale of tens to hundreds of nanoseconds. Umbrella sampling and related methods in principle are accurate, but they require a specific reaction coordinate (e.g. the depth of the center of mass of a protein domain in a membrane) and convergence of all motions that are not part of the reaction coordinate. The latter requirement is almost impossible to fulfil for large conformational changes. An approximate method to study the effect of conformational changes anyway is to force these changes and observe what happens. Several groups have developed this approach in the literature (see refs. 24 & 25 for recent reviews). The simulation of the potassium channel KvAP below is an example. A second approach to studying conformational changes is discussed below as well, where the ATP-binding domains of an ABC transporter undergo conformational changes upon manually introducing ATP, or the maltose binding protein opens and closes depending on the presence or absence of maltotriose.

Problem 1. The distribution of small molecules in a lipid bilayer

The membrane environment is inhomogeneous, with large gradients in density, available free volume and polarity on a length scale of ca. 3 nm. The partitioning behaviour or distribution of small molecules in such a complex environment is of interest from a number of perspectives. Small molecules such as water, nitrogen, oxygen, and carbon dioxide often move across the cell membrane primarily by passive diffusion, which is primarily determined by their partitioning behaviour.^26-28 Many hydrophobic drug molecules enter the cell through passive diffusion across the cell membrane, and understanding and fine-tuning their partitioning behaviour has important implications for their pharmacokinetics and bioavailability. Environmental pollutants like pentachlorophenol, a wood preservative in common use until recently, accumulate in lipids, and the interpretation of fluorescence experiments using lipid-derived dyes depends on where these dyes are actually located in the membrane. Membrane protein folding is also related to partitioning behaviour, in this case of amino acid side chains.²⁹ It is not obvious how to relate bulk thermodynamic partitioning experiments to partitioning into bilayers, but detailed computer simulations can be used to interpret these experiments, elucidate the relative importance of entropic and enthalpic contributions, and relate these to properties such as chain ordering, free volume distribution, polarity, and shape of the small molecules partitioning into the membrane. It is also possible to obtain sufficiently accurate experimental information to validate the simulations by comparing their average properties to experimentally measured values.

We have chosen a set of small molecules to study, including pentachlorophenol,³⁰ pyrene,³¹ hexane,³² and benzyl-compounds.³³ Pyrene and hexane are of particular interest. Pyrene is a fluorescent dye we studied both by MD simulation and by solid state NMR spectroscopy to validate the results of the MD simulation and to complement the NMR data. For hexane, accurate thermodynamic data as well as the distribution in a bilayer are known, making this an excellent system to test simulations and further develop our methodology.

Quadrupolar splittings from ²H-NMR spectra of deuterated pyrene-d₁₀ in an oriented lipid bilayer give information about the orientation of C-D bonds with respect to the membrane normal. From MD simulations, such geometric information is directly accessible from the trajectories because we know at any time the location of all atoms. The data from MD trajectories and NMR spectra can be compared straightforwardly by defining molecular and bond order parameters. In an MD simulation with pyrene molecules in different locations in the bilayer, pyrene rapidly moves towards an average position and orientation just below the lipid carbonyl groups. Figure 1 shows a snapshot before and after the simulation, with the different locations of pyrene. It is straightforward to calculate the order parameters describing the orientation of C-H bonds with respect to the membrane. The same orientation can be measured from deuterium splittings from solid-state NMR experiments under the same conditions (temperature, hydration level, concentration of pyrene, type of lipid). We found that the orientation of pyrene in simulation and experiment agrees almost exactly when the last five nanoseconds of the simulation were used to calculate the orientation. During this time the average orientation of pyrene no longer changed. Any other period of five nanoseconds, however, gave poor agreement with experiment. The results from simulation and NMR show that the normal of the molecular plane is aligned nearly perpendicular to the bilayer normal. The long axis of pyrene lies preferentially parallel to the bilayer normal within a range of ±30°. The results from the two different methods are remarkably consistent. The good agreement can be explained by the fact that the different kind of motions of a pyrene molecule are already averaged within a few nanoseconds, which is the timescale covered by the MD simulation. These results show that MD simulations can give accurate results for the orientation of organic molecules, and provide additional detail that is not readily accessible by other methods.

The pyrene simulations in one sense are straightforward: one adds pyrene to the simulation model of the bilayer and waits for the molecules to reach equilibrium positions. This approach answered the questions we were interested in, but by itself does not give any real insight into the thermodynamics of the interactions between pyrene and the bilayer. Although the distribution can be converted into partition coefficients and free energy profiles, straightforward simulations really only identify the most favourable location in the membrane and do not provide accurate estimates of the relative likelihood of finding pyrene at different places in the bilayer.

For hexane, we calculated the exact distribution in the bilayer, which corresponds to the potential of mean force or free energy profile, using umbrella sampling. By calculating the PMF at three temperatures with high statistical accuracy, we also obtained enthalpy and entropy profiles. The results of these calculations are shown in Figure 2. Figure 2A shows a snapshot of the simulation system. Figure 2B shows the density profile of the bilayer, which essentially gives the average composition of the system as a function of distance from the center of the bilayer. The shape of this profile has been discussed in great detail in the literature and can be measured experimentally.³⁴ Figure 2C shows the new results: the free energy, enthalpy and entropy profiles. Clearly hexane partitions preferentially to the center of the bilayer, in good agreement with experiment.³⁵ The free energy profile is relatively flat from 0.0 nm to around 1.5 nm where it begins to increase rapidly, consistent with the width of the experimental distribution. The free energy exhibits a maximum in the head group region (approximately 2.25 nm) before decreasing slightly and leveling off as water reaches its bulk density. The umbrella sampling calculations show that the free energy of locating hexane in the center of the bilayer is approximately 24 kJ mol^-1 more favourable than bulk water. This change is driven almost entirely by entropy with only a small enthalpic component, which is consistent with the hydrophobic effect. Thus for the partitioning of hydrophobic solutes, the very center of a lipid bilayer appears to have very similar properties to a bulk alkane such as octane.

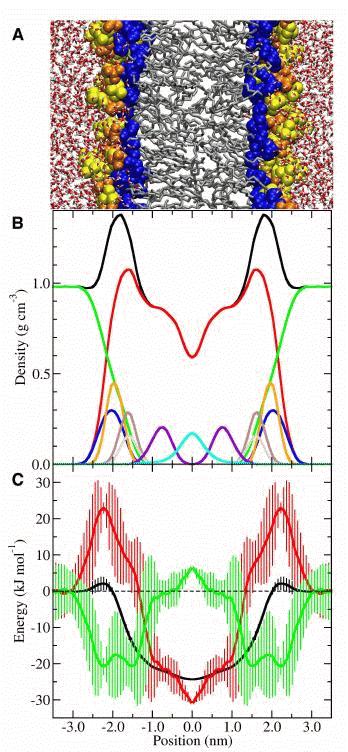
Figure 2. Free energy of hexane in a DOPC bilayer. A: Snapshot of the lipid bilayer system used (red and white tubes - water; yellow spheres - choline; orange spheres - phosphate; blue spheres - glycerol and carbonyl; grey tubes - alkane chains). B: Average partial density profiles for various functional groups (black - total density; red - lipid; green - water; blue - choline; orange - phosphate; brown - glycerol; grey - carbonyl; purple - double bonds; cyan - methyl). C: Free energy of partitioning a hexane molecule from bulk water (black - free energy; red - entropic component of free energy, -TΔS; green - enthalpic component of free energy, ΔH). Vertical bars represent standard errors obtained by measuring the asymmetry between leaflets in the bilayer. Reproduced with permission from ref. 32.

Partitioning into the acyl chains becomes increasingly unfavourable moving from the low density, unordered region (0.0 nm) to the high density, highly ordered region (∼1.4 nm). This is driven by opposing trends in the enthalpy and entropy. The enthalpy becomes more favourable, while the entropy becomes more unfavourable with increasing acyl chain density.

The pyrene and hexane studies demonstrate two important aspects of computer simulations. In both cases, there are global, average results that can be measured experimentally: the average orientation relative to the normal on the membrane in the case of pyrene (but not the depth in the membrane, nor the distribution of orientations), and the free energy of transfer, distribution, and average hexane order parameter in the case of hexane. These validate the simulations, but in addition the simulations give additional, very detailed results that are not accessible by experiments. In both cases, the experiments are much more complicated than the simulations, and the simulations will get cheaper (both in computer time with its associated cost, and in human effort) over time at what will most likely be a very rapid rate compared to the experiments. One practical area where this type of simulations will be useful is in investigating the distribution and permeation of hydrophobic drug molecules.

Problem 2. The mechanism of electroporation

The interaction of electric fields with membranes is of fundamental interest in biology as well as in a number of engineering applications. At a more subtle level, the membrane potential controls the operation of voltage-gated channels,³⁶ the basis of nerve transduction. Here, however, we consider what happens when a very large electric field is placed across membranes, such as used in electroporation in the lab to introduce foreign molecules into cells or industrially for e.g. water treatment.

In the past few years electroporation has seen a surge in interest due to engineering advances that allow ultrashort very powerful pulses of 5-100 ns length that primarily affect organelles instead of the plasma membrane of cells, suggesting new ways to use electroporation in drug delivery and gene therapy.³⁷ Several recent papers have investigated electroporation in detail by simulation.^{13, 14,38-40} Although there are technical issues still under discussion, one of the key results is likely to be quite robust to changes in methods: Figure 3 shows snapshots of the formation of a pore in a dioleoylphosphatidylcholine bilayer. Animations of this process are available online, linked from ref. 13 at http://www.biomedcentral.com. Pores form from small water defects, which occur more commonly near head group defects, where the choline group of the lipid is located nearer the glycerol backbone region than normal. Initially, there is no clear sign of head group defects or other irregularities at the site of pore formation, only a few hundred picoseconds later. Water molecules are occasionally found in the interior of the membrane, which is normally, in the absence of applied electric fields, a very rare occasion. Such water molecules may form hydrogen-bonded chains of several water molecules, which do not have to lead to pores. Initially, a deformation of the head groups is seen, with water defects forming at the same time. The water defects begin to span the bilayer, and head groups start moving towards this pore (Figure 3A&B). This focuses the electric field across the defect, and the process accelerates. The pore then expands and becomes lined with lipid headgroups (3C), although it takes some time before the head groups are evenly distributed over the pore 'surface'. Although in the final snapshot lipid chains are still exposed to water (3D), this is not unlike the distribution of head groups in an unperturbed bilayer. This atomistic description enables detailed analyses of the driving forces for pore formation. It appears that a key driving force is the motion of dipoles (water molecules and lipid head groups) in the strong field gradients at the interface. There always is a field gradient at the interface, even in the absence of an applied electric field, but this appears to be balanced by other forces that give a stable interface. In the presence of an electric field, this balance is broken, and pore formation is the way to minimize the total free energy of the system in the presence of an applied electric field of sufficient strength.¹³

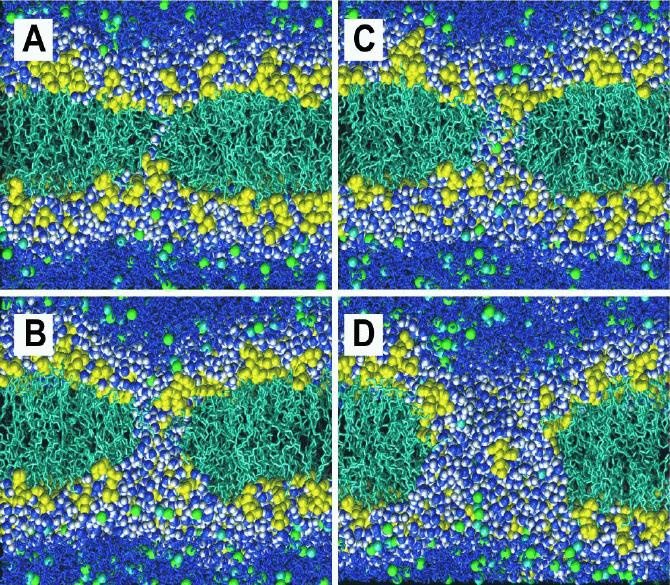
Figure 3. Snapshots of pore formation in the DOPC bilayer, with an applied field of 0.5 V/nm in the presence of 1 M NaCl (right): A) 5330 ps, B) 5450 ps, C) 5500 ps, D) 5700 ps. The lipid headgroups are shown in yellow, the chains in cyan, chloride ions space-filling in green, sodium ions in cyan; water is shown as dark blue and white space-filling in the interface region and the pore, as dark blue bonds elsewhere. The potential is positive at the top of each snapshot relative to the bottom. Adapted from ref. 48.

Thus the simulations show how a pore forms in atomistic detail, starting from water defects involving one and then a few water molecules, with final pores involving significant rearrangement of lipids to form a toroidal, doughnut-shaped, pore that is lined with head groups. Current work is aimed at a better characterization of the kinetics of pore formation, the translocation of phosphatidylserine lipids in a mixed bilayer (a marker of apoptosis), and forging a stronger link with experiments with nanosecond length high field pulses (the same time scale as the simulations!).⁴¹ A recent paper showed similar pore formation, but in the presence of DNA and of a peptide-nanopore.⁴⁰ Clearly, pore formation is linked to the likelihood of defects forming, which can be either aided or prevented by the presence of other molecules in the lipid bilayer. This can be tested by further simulations.

Problem 3: Molecular dynamics simulations to investigate the KvAP crystal structure and a proposed gating mechanism

It has proven difficult to determine the structure of membrane proteins in atomistic detail, although recent progress has been impressive. Membrane proteins present a particular challenge because in many cases their structural integrity appears to depend on the bilayer environment. One consequence of this is that membrane proteins may have a tendency to adopt distorted structures when solubilized in detergent. From a physiological point of view, many membrane proteins of interest carry out tasks that require significant conformational changes, including signaling, transport, and regulated ion conduction. A crystal structure typically captures a single state of a protein. Thus there are at least two reasons to consider computer simulations of membrane protein structures. First, simulations may help identify parts of a membrane protein crystal structure that may be distorted due to the surfactant environment. Second, simulations, possibly combined with other modelling methods, may help to identify different functional states of a protein based on an experimental structure of one state.

The voltage-gated potassium channel KvAP is a high-profile example of a membrane protein structure^42,43 that caused substantial discussion based on unexpected features that may have been due to crystallization artifacts.^44,45 Voltage-gated potassium, sodium, and calcium channels all have a similar structure, consisting of four similar or identical domains that surround a central pore. In potassium channels, two helices, called S5 and S6, from each of the four domains form the actual pore, whereas the first four helices S1 – S4 form the voltage sensor. S4 is particularly important, because it contains the conserved arginine residues that confer voltage sensitivity to the domain. Upon gating, about 12 ‘gating charges’ cross the transmembrane potential difference, corresponding to the arginines on S4. A major question has been what the molecular motions involved in voltage gating are. A large body of experimental work led to several models that all had in common that S1-S4 are approximately parallel to S5 and S6, spanning the membrane.^45,46

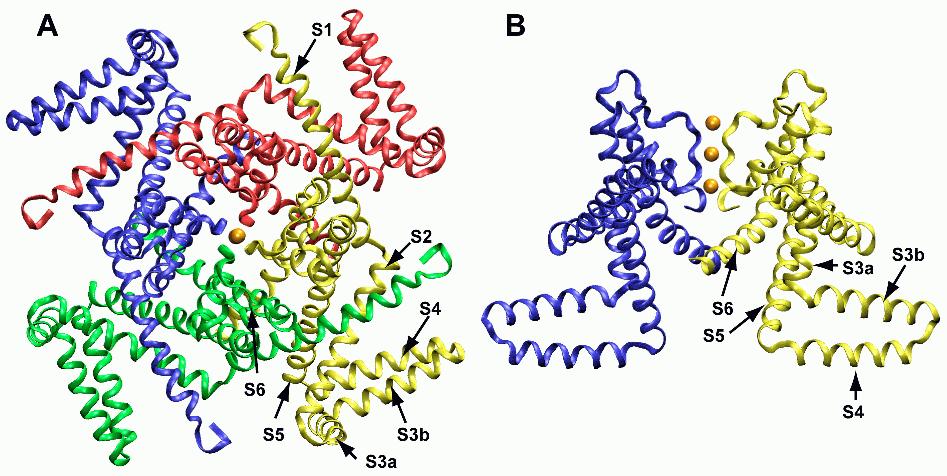
Figure 4. A: Crystal structure of the KvAP voltage-gated potassium channel. The four subunits are coloured green, yellow, red, and blue; potassium ions are orange. In B, a side view of two subunits is shown, with labelled helices in the yellow subunit. The S3b/S4 helices form the paddle. Figure 5 shows the location of the lipid bilayer.

The structure of KvAP, however, showed an almost detached S1-S4 ‘paddle’ domain that seemed to lie at the surface of the membrane (Figures 4, 5A). A separate structure of just the S1-S4 domain was also solved.⁴³ KvAP was rapidly recognized as deformed, but the separate paddle structure provides additional information. Based on the crystal structures, MacKinnon and co-workers suggested a model in which the S1-S4 paddle is attached to the S5 helix at the intracellular side and sweeps across the membrane so that the tip of the paddle moves between the intracellular and extracellular side of the membrane in gating.⁴² This exposes four arginines per subunit to the lipid, which is a highly controversial idea. The motion of the paddle also seems to conflict with other experimental data that measured distances between residues using fluorescence or by engineering metal binding sites.

Some aspects of the proposed ‘paddle’ mechanism can be tested in a simulation. First, we ask what happens if the crystal structure is simulated in a lipid bilayer. Second, we consider changes in the protein when the paddle is pulled through the membrane by an artificial force that is supposed to mimic the effects of a change in transmembrane potential.

Equilibrium simulations of KvAP

After equilibration of the lipids and water around the crystal structure there is large curvature of the bilayer such that the central pore (S5-S6) and the voltage sensor (S3-S4) are surrounded by the hydrophobic membrane while the arginine residues are positioned at the interface. Upon relaxation of the crystal structure the paddles rapidly move into the hydrophobic interior (2 ns) and remain there for the duration of the simulation (Figure 5B). This large change of the paddle location and structure, which results in an overall RMSD for the whole tetramer of ∼0.6 nm, does not however influence the conformation of the central pore. In a model that combines the isolated paddle structure with the pore domain of the full KvAP structure, this change does not occur (Figure 5C). Thus the simulations suggest that the KvAP crystal structure is significantly deformed compared to what the protein structure would be in a lipid bilayer.⁴⁷

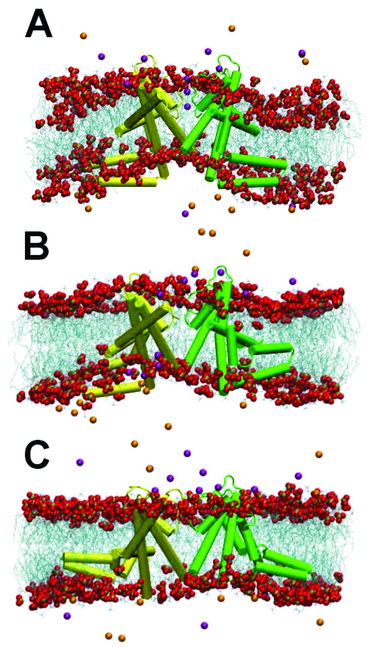
Figure 5. Snapshots of the KvAP structure in a simulation in a DMPC bilayer. A: Starting structure, using the crystal structure of KvAP. B: Final structure after 10 ns of simulation. C: Final structure after 10 ns of the “nimera” simulation, starting from a model that combines the separate paddle structure with the pore region of the full structure. Only two of the four subunits are shown, one in yellow and one in green. Helices are shown as solid cylinders, loops as lines. Lipid chains are shown as cyan lines with phosphate and oxygen atoms shown in space fill and coloured gold and red respectively. Chloride and potassium ions are shown as orange and purple spheres.

Pulling the paddles through the membrane

If we assume that the resulting simulation structure after 10 ns, or the model including the isolated paddle, are realistic, we can ‘test’ the paddle model by simulation.⁴⁸ Although it is possible to apply electric fields in a simulation, the fields required to see any effects on a nanosecond time scale are very large and physiologically not relevant.⁴⁹ Instead, we chose to literally ‘pull’ the paddles through the ‘membrane’, which for this occasion for simplicity was modeled as a 3 nm thick slab of alkane. Effectively, we attach a spring to the tips and pull the spring through the membrane during a 10 ns simulation. A caveat with this type of simulation is that a realistic time scale for simulations of 10 ns is very short compared to the actual rate at which a large protein domain would move, although this rate is not known exactly.

Despite the high pulling rate, the S5, S6 and pore helices are very stable (data not shown, see ref. 48). The channel appears to be partially open in the starting structure, and the shape and the size of the pore undergo only minor modifications during the simulation. The effect of the motion of the paddles is not propagated immediately – the opening of the channel would occur on a longer time scale. This might be reasonable as voltage gating can be described by a model that has four independent conformational changes, presumably the individual voltage sensors of each of the four domains, followed by a collective step that actually opens the channel.⁵⁰

Visual inspection of the trajectory confirms that the paddles undergo mainly a rigid domain motion, with S2 acting as a hinge for the rotation of S3b and S4, in agreement with the suggestion of Jiang et al.⁴³ Both in the crystallographic structure of the full protein and in the starting structure of our model the five conserved arginine residues in the S4 helix (R117, R120, R123, R126, R133 in KvAP; R362, R365, R368, R371 and R377 in Shaker) are solvent-exposed. As the simulation proceeds, S4 moves from the octane-water interface to the membrane-mimicking environment. R117 enters the octane slab before the others, followed by R120, R123 and R126.

The most interesting result of our experiment is the formation of water and ion defects upon pulling the paddle into the membrane interior (Figure 6). The exposed arginine side chains drag several hydrating water molecules with them into the octane slab. After approximately 4 ns of simulation, the first four arginines are completely inserted into the octane slab, although they are still surrounded by water. Partial desolvation of R117 and R120 starts only 1.5 ns later, while R123 and R126 retain their full solvation shell until the end of the simulation. Since the water pockets surrounding the arginines are directly connected to the bulk water, chloride ions penetrate deep into the octane slab and form short-lived ion pairs with the positively charged side chains. The number of chloride ions interacting with the guanidinium groups increases during the simulations, starting from 0.1 ions per arginine and ending with ∼0.8 and ∼0.6 ions for R117 and R120 respectively. One likely explanation is that the hydrated chloride ions partially neutralize the high positive charge on S4, making it less difficult to cross the hydrophobic environment.

The simulations show major changes in the crystal structure when the structure is embedded in a bilayer, suggesting strongly – based on simulation only, although there is ample experimental information to argue the same thing – that the crystal structure is not in a physiological state. If we test the hypothesis that pulling the paddle through the membrane corresponds to the conformational change in gating, our simulations suggest substantial water defects and the potential for ions to move with the gating charge arginines. More recent models of Kv’s are more sophisticated,^51,52 and more recent structures of KvAP^53,54 and Kv1.2^55,56 also refine the picture that is emerging, but this is still a reasonable illustration of the use of simulations based on experimental information and the original KvAP structures only.

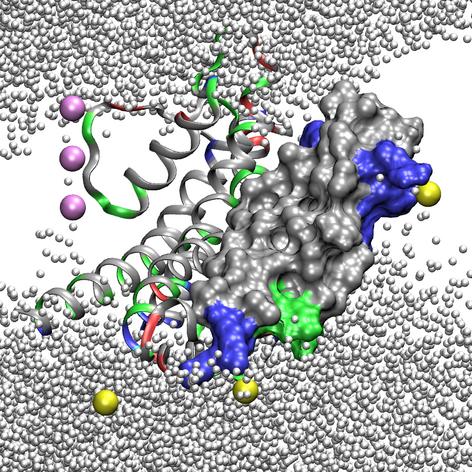
Figure 6. Water defects surrounding the KvAP “paddle” when the paddle is pulled deeper into the membrane. Snapshot from the steered MD simulation (at time = 9.5 ns). The residues are coloured according to type: red – basic, blue – acidic, green – polar, grey – non-polar. The voltage-sensing paddle (S3b-S4) is shown in a surface representation. Water is shown as small white spheres; potassium is pink, and chloride is yellow. R117 and R120 share one solvated chloride ion, and drag substantially less water molecules into the membrane compared to R123 and R126. Reproduced from ref. 48.

Problem 4: the dynamics of the ABC transporter BtuCD/BtuF

ATP-Binding Cassette (ABC) transporters are modular mechanical machines that couple the hydrolysis of ATP with the transport of molecules against a concentration gradient.⁵⁷ They consist of 2 nucleotide binding domains (NBDs), 2 transmembrane domains, and optional additional domains, organized in a varying number of polypeptide chains. Mutations in the genes encoding many of the 48 ABC transporters of human cells are associated with several diseases, including cystic fibrosis, adrenoleukodystrophy, Tangier disease, and obstetric cholestasis. Crystal structures of the ABC transporters MsbA^58-61 and BtuCD⁶² have been determined recently, as well as structures of the periplasmic binding protein BtuF.^63,64 In addition, a large number of solution structures of the separate nucleotide binding domains as well as periplasmic binding proteins is available. Figure 7 summarizes the vitamin B12 import system, consisting of an outer membrane receptor (BtuB), a periplasmic binding protein (BtuF), and the ABC transporter (BtuCD). Combined, these structures enable different computational approaches aimed at understanding a key question in the mechanism of an ABC transporter: how does ATP hydrolysis get translated into active transport of a broad range of substrates? For molecular dynamics simulations, the large size of these proteins and the long time-scales involved in function are a challenge. Nevertheless, we have obtained encouraging results from simulations of nucleotide binding domains, periplasmic binding proteins, and initial simulations of the full BtuCD transporter.

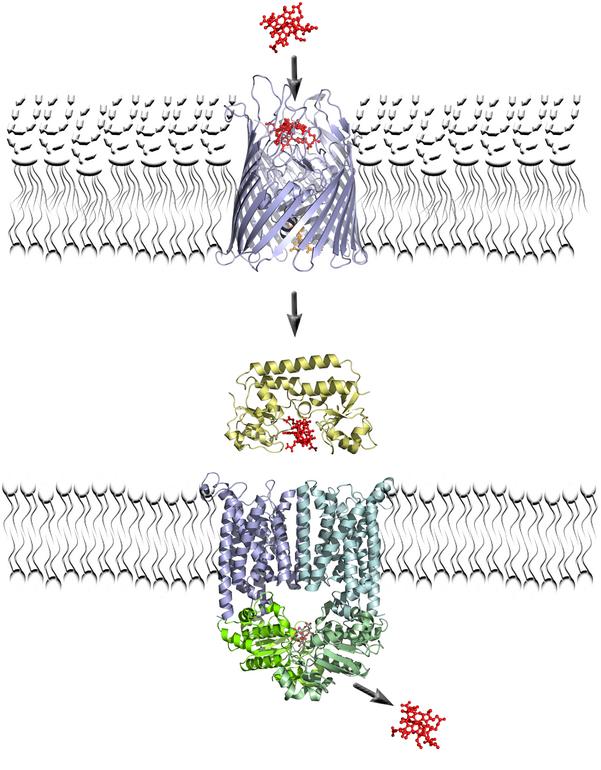
Figure 7. Schematic of the E. coli vitamin B12 importer system. Vitamin B12 is red; the beta-barrel is BtuB, the outer membrane receptor for B12; the periplasmic binding protein BtuF is yellow; the two transmembrane domains of BtuCD are blue, the two NBDs are green. ATP binds at the interface between the two NDBs. The transport pathway through BtuCD is not known with certainty. Image courtesy Dr. C. Kandt.

The periplasmic binding protein MBP

The maltose/maltodextrin-binding protein (MBP) serves as an initial high-affinity binding component in the periplasm that delivers the bound sugar into the cognate ABC transporter MalFGK₂. We have investigated the domain motions induced by the binding of the ligand maltotriose into the binding cleft using molecular dynamics simulations. This is a particularly interesting test case for simulations, because crystal structures of the open state without maltotriose and the closed state with maltotriose are available. If the simulations are accurate, they should be able to reproduce the large-scale domain motions of MBP if we remove maltotriose from the closed state (it should open), or add it to the open state (it should close). This is indeed what happens in simulations on a time-scale of tens of nanoseconds.⁶⁵ Additional unpublished simulations of ribose binding protein and BtuF find similar results, although the time scales required are almost an order of magnitude longer (Stockner, Kandt, and Tieleman, unpublished). The domain motions of periplasmic binding proteins may play a critical role in transport. Our current hypothesis is that binding of the periplasmic binding protein to the ABC transporter forces a conformational change that reduces the affinity of the ligand for the binding protein, effectively releasing it into the transporter. This remains to be tested.

Nucleotide binding domain dynamics in BtuCD

The BtuCD structure was solved with tetraorthovanadate bound to the ATP-binding sites, in such a way that the two NBDs in the crystal structure do not directly interact but face each other in what appears a reasonable physiological orientation.⁶² As an initial attempt to use the crystal structure to understand how the two NBDs interact with each other and potentially with the transmembrane domains, we compared two simulations of BtuCD in a lipid/water environment. In the first, we simply removed the vanadate. In the second, we docked MgATP in the two binding sites, based on a comparison of the BtuCD structure with a crystal structure of the MalK dimer with ATP bound.^66,67

In the absence of MgATP, no substantial interactions between the two NBDs are observed. In contrast, docking of ATP to the catalytic pockets progressively draws the two cytoplasmic nucleotide-binding cassettes towards each other (Figure 8). Moreover, occlusion of ATP at one catalytic site is mechanically coupled to opening of the nucleotide-binding pocket at the second site. We propose that this asymmetry in nucleotide binding behaviour at the two catalytic pockets may form the structural basis by which the transporter is able to alternate ATP hydrolysis from one site to the other. Interestingly, in simulations of the MalK dimer, without its transmembrane domain (whose structure is not known), the two binding sites interact symmetrically (Oloo and Tieleman, in preparation). We also observe substantial motions of the transmembrane domains in BtuCD, at the same time as interactions between the NBDs. It is encouraging that some motions of these large domains as a whole are captured in simulations on a time scale of tens of nanoseconds. We are currently pursuing similar simulations as well as simulations that include a form of biasing to move either the NBDs or the transmembrane domains, with the hope of observing the response of the domains that are not being moved explicitly. With current computer capabilities it is easier to perform multiple copies of simulations to increase the statistical significance of observations based on trajectories. It seems certain that we will see a rapidly growing number of computational studies on this interesting class of proteins.

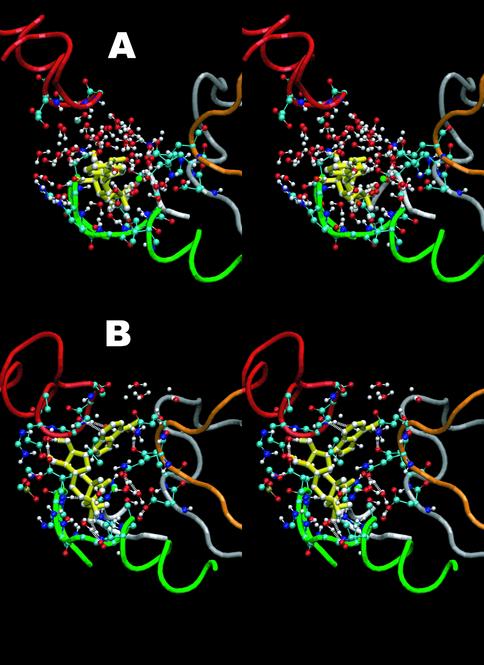
Figure 8. Stereographic images depicting the optimization of binding of one of the two docked MgATP molecules during the simulation. (A) Docked MgATP at time 0ns. (B) MgATP coordination at 15ns. The backbone of segments containing the Walker A, Walker B and Q-loop sequences of the NBD onto which the nucleotide was initially docked are shown as green, silver and orange tubes respectively. The segment hosting the signature motif from the opposing NBD is similarly rendered in red. MgATP is shown in yellow and solvent water molecules in red and white. Reproduced with permission from ref. 15.

Outlook

In the past few years, growth in the number of simulation studies and the complexity of the proteins simulated has been phenomenal. Simulations of pure lipids are now investigating phenomena on much larger length (10–30 nm) and time scales (hundreds of nanoseconds) and can be compared more directly to experiment and theoretical work at mesoscopic scales. The availability of fast software and relatively cheap computers will no doubt lead to a further increase in the complexity of the systems that can be simulated. It should also lead to increased methodological development and more extensive control simulations to improve the statistical accuracy of phenomena observed. Simulations are generating questions that can be tested experimentally, which will no doubt lead to increasingly stronger links with experiment. The recent growth in the number of high-resolution membrane protein structures is an exciting development. Simulations can provide additional dynamic details of the static snapshots given by membrane protein structures and can be used to investigate and build models of other conformational states.

It is worth reflecting on the time and effort spent on a particular type of simulation. Eight years ago, it took 6 months to create a starting model of the bacterial porin OmpF in a lipid bilayer, and another 6 months on a very expensive computer to simulate its motions for 1 ns.⁶⁸ Recently we repeated a very similar calculation in a day or two, using desktop computers. All simulations described were done with the GROMACS software,⁶⁹ which can be freely downloaded from http://www.gromacs.org. Most of the examples I have given in this paper would be considered complicated simulations by the standards of their publication dates (2004-2006), but ongoing simulations that build on the hexane distribution, electroporation, and the dynamics of ABC transporters are already a magnitude or more complex in scope, time scale, and different scenarios. I believe increasingly in the future computational studies can provide a valuable contribution to many problems in biochemistry, biophysics and related areas, often as a small part of an integrated approach to solving a specific problem that combines experiment and simulation.

Acknowledgements

DPT is an Alberta Heritage Foundation for Medical Research Senior Scholar, a CIHR New Investigator, and Sloan Foundation Fellow. This work was supported by CIHR and NSERC, using WestGrid computational facilities. I thank former and present members of my group for their roles in the work described here, in particular: Justin MacCallum (hexane), Barbara Hoff and collaborators in Karlsruhe (pyrene), Dr. Luca Monticelli and Kindal Robertson (KvAP), Eliud Oloo, Dr. Christian Kandt, and Dr. Thomas Stockner (ABC transporters).

References

1.  Tieleman DP, Marrink SJ, Berendsen HJC. A computer perspective of membranes: Molecular dynamics studies of lipid bilayer systems. Biochim. Biophys. Acta. 1997; 1331: 235-270.

2.  Ash WL, Zlomislic MR, Oloo EO, Tieleman DP. Computer simulations of membrane proteins. Biochim. Biophys. Acta. 2004; 1666: 158-189.

3.  Tieleman DP, Biggin PC, Smith GR, Sansom MS. Simulation approaches to ion channel structure-function relationships. Q. Rev. Biophys. 2001; 34: 473-561.

4.  Noskov SY, Berneche S, Roux B. Control of ion selectivity in potassium channels by electrostatic and dynamic properties of carbonyl ligands. Nature. 2004; 431: 830-834.

5.  Beckstein O, Biggin PC, Bond P, et al. Ion channel gating: insights via molecular simulations. FEBS Lett. 2003; 555: 85-90.

6.  Berneche S, Roux B. Energetics of ion conduction through the K⁺ channel. Nature. 2001; 414: 73-77.

7.  Aqvist J, Luzhkov V. Ion permeation mechanism of the potassium channel. Nature. 2000; 404: 881-884.

8.  Tajkhorshid E, Nollert P, Jensen MO, et al. Control of the selectivity of the aquaporin water channel family by global orientational tuning. Science. 2002; 296: 525-530.

9.  de Groot BL, Grubmuller H. Water permeation across biological membranes: Mechanism and dynamics of aquaporin-1 and GlpF. Science. 2001; 294: 2353-2357.

10.  Chakrabarti N, Tajkhorshid E, Roux B, Pomes R. Molecular basis of proton blockage in aquaporins. Structure (Camb). 2004; 12: 65-74.

11.  Stevens MJ, Hoh J, Woolf TB. Insights into the molecular mechanism of membrane fusion from simulation: evidence for the association of splayed tails. Phys. Rev. Lett. 2003; 91: 188102.

12.  Marrink SJ, Mark AE. The mechanism of vesicle fusion as revealed by molecular dynamics simulations of small phospholipid vesicles. J. Am. Chem. Soc. 2003; 125: 11144-11145.

13.  Tieleman DP. The molecular basis of electroporation. BMC Biochem. 2004; 5: 10.

14.  Tieleman DP, Leontiadou H, Mark AE, Marrink SJ. Simulation of pore formation in lipid bilayers by mechanical stress and electric fields. J. Am. Chem. Soc. 2003; 125: 6382-6383.

15.  Oloo EO, Tieleman DP. Conformational transitions induced by the binding of MgATP to the vitamin B12 ATP binding cassette transporter, BtuCD. J. Biol. Chem. 2004; 279: 45013-45019.

16.  Gumbart J, Wang Y, Aksimentiev A, Tajkhorshid E, Schulten K. Molecular dynamics simulations of proteins in lipid bilayers. Current Opinion in Structural Biology. 2005; 15: 423-431.

17.  Van Gunsteren WF, Berendsen HJC. Computer-Simulation of Molecular-Dynamics - Methodology, Applications, and Perspectives in Chemistry. Angewandte Chemie-Intl. Ed. 1990; 29: 992-1023.

18.  Karplus M, McCammon JA. Molecular dynamics simulations of biomolecules. Nature Struct. Biol. 2002; 9: 646-652.

19.  Schlick T. Molecular modeling and simulation. New York: Springer; 2002.

20.  Leach AR. Molecular modelling: principles and applications: Longman; 2001.

21.  Ponder JW, Case DA. Force fields for protein simulations. Adv. Protein Chem. 2003; 66: 27-85.

22.  Kollman P. Free-Energy Calculations - Applications to Chemical and Biochemical Phenomena. Chem. Rev.1993; 93: 2395-2417.

23.  Berneche S, Roux B. A microscopic view of ion conduction through the K⁺ channel. Proc. Natl. Acad. Sci. U S A. 2003; 100: 8644-8648.

24.  Tajkhorshid E, Aksimentiev A, Balabin I, et al. Large scale simulation of protein mechanics and function. Protein Simulations. Vol 66; 2003:195-+.

25.  Schlick T, Skeel RD, Brunger AT, et al. Algorithmic challenges in computational molecular biophysics. J. Comp. Phys. 1999; 151: 9-48.

26.  Marrink SJ, Berendsen HJC. Simulation of water transport through a lipid membrane. J. Phys. Chem. 1994; 98: 4155-4168.

27.  Bemporad D, Luttmann C, Essex JW. Computer simulation of small molecule permeation across a lipid bilayer: dependence on bilayer properties and solute volume, size, and cross-sectional area. Biophys J. 2004; 87: 1-13.

28.  Jedlovszky P, Mezei M. Calculation of the free energy profile of H2O, O2, CO, CO2, NO, and CHCl3 in a lipid bilayer with a cavity insertion variant of the Widom method. J. Am. Chem. Soc. 2000; 122: 5125-5131.

29.  Wimley CW, White SH. Experimentally determined hydrophobicity scale for proteins at membrane interfaces. Nature Struct. Biol. 1996; 3: 842-848.

30.  MacCallum JL, Mukhopadhyay P, Luo H, Tieleman DP. Large scale molecular dynamics simulations of lipd-drug interactions. Paper presented at: Proceedings of the 17th Annual International Symposium on High Performance Computing Systems and Applications and the OSCAR Symposium, 2003; Sherbrooke.

31.  Hoff B, Strandberg E, Ulrich AS, Tieleman DP, Posten H. 2H-NMR study and molecular dynamics simulation of the location, alignment, and mobility of pyrene in POPC bilayers. Biophys. J. 2005; 88: 1818-1827

32.  MacCallum JL, Tieleman DP. Computer simulation of the distribution of hexane in a lipid bilayer: Spatially resolved free energy, entropy, and enthalpy profiles. J. Am. Chem. Soc. 2006; 128: 125-130.

33.  Ahumada H, Montecinos R, Tieleman DP, Weiss-Lopez BE. Orientation and dynamics of benzyl alcohol and benzyl alkyl ethers dissolved in nematic lyotropic liquid crystals. H-2 NMR and molecular dynamics simulations. J. Phys. Chem. A. 2005;109(30):6644-6651.

34.  Nagle JF, Tristram-Nagle S. Structure of lipid bilayers. Biochim. Biophys. Acta-Reviews on Biomembranes. 2000; 1469: 159-195.

35.  White SH, King GI, Cain JE. Location of hexane in lipid bilayers determined by neutron diffraction. Nature. 1981; 290: 161-163.

36.  Hille B. Ion channels of excitable membranes. third ed. Sunderland: Sinauer Associates, Inc.; 2001.

37.  Weaver JC. Electroporation of biological membranes from multicellular to nano scales. IEEE Transactions on Dielectrics and Electrical Insulation. 2003; 10: 754-768.

38.  Gurtovenko AA, Vattulainen I. Pore formation coupled to ion transport through lipid membranes as induced by transmembrane ionic charge imbalance: Atomistic molecular dynamics study. J. Am. Chem. Soc. 2005; 127: 17570-17571.

39.  Hu Q, Joshi RP, Schoenbach KH. Simulations of nanopore formation and phosphatidylserine externalization in lipid membranes subjected to a high-intensity, ultrashort electric pulse. Phys. Rev. E. 2005; 72: 031902.

40.  Tarek M. Membrane electroporation: A molecular dynamics simulation. Biophys. J. 2005; 88: 4045-4053.

41.  Vernier PT, Ziegler MJ, Sun Y, Chang WV, Gundersen MA, Tieleman DP. Nanopore formation and phosphatidylserine externalization in a phospholipid Bilayer at high transmembrane potential. J. Am. Chem. Soc. 2006; in press.

42.  Jiang Y, Ruta V, Chen J, Lee A, MacKinnon R. The principle of gating charge movement in a voltage-dependent K⁺ channel. Nature. 2003; 423: 42-48.

43.  Jiang Y, Lee A, Chen J, et al. X-ray structure of a voltage-dependent K⁺ channel. Nature. 2003; 423: 33-41.

44.  Cohen BE, Grabe M, Jan LY. Answers and questions from the KvAP structures. Neuron. 2003; 39: 395-400.

45.  Bezanilla F. The voltage-sensor structure in a voltage-gated channel. TIBS. 2005; 30: 166-168.

46.  Bezanilla F, Perozo E. The voltage sensor and the gate in ion channels. Adv. Protein Chem. 2003; 63: 211-241.

47.  Tieleman DP, Robertson KM, Maccallum JL, Monticelli L. Computer simulations of voltage-gated potassium channel KvAP. Intl. J. Quant. Chem. 2004; 100: 1071-1078.

48.  Monticelli L, Robertson KM, MacCallum JL, Tieleman DP. Computer simulation of the KvAP voltage-gated potassium channel: steered molecular dynamics of the voltage sensor. FEBS Lett. 2004; 564: 325-332.

49.  Tieleman DP, Berendsen HJ, Sansom MS. Voltage-dependent insertion of alamethicin at phospholipid/water and octane/water interfaces. Biophys. J. 2001; 80: 331-346.

50.  Horn R. Conversation between voltage sensors and gates of ion channels. Biochemistry. 2000; 39: 15653-15658.

51.  Posson DJ, Ge PH, Miller C, Bezanilla F, Selvin PR. Small vertical movement of a K⁺ channel voltage sensor measured with luminescence energy transfer. Nature. 2005; 436: 848-851.

52.  Chanda B, Asamoah OK, Blunck R, Roux B, Bezanilla F. Gating charge displacement in voltage-gated ion channels involves limited transmembrane movement. Nature. 2005; 436: 852-856.

53.  Ruta V, Chen JY, MacKinnon R. Calibrated measurement of gating-charge arginine displacement in the KvAP voltage-dependent K⁺ channel. Cell. 2005; 123: 463-475.

54.  Lee SY, Lee A, Chen JY, MacKinnon R. Structure of the KvAP voltage-dependent K⁺ channel and its dependence on the lipid membrane. Proc. Natl. Acad. Sci. 2005; 102: 15441-15446.

55.  Long SB, Campbell EB, MacKinnon R. Crystal structure of a mammalian voltage-dependent Shaker family K⁺ channel. Science. 2005; 309: 897-903.

56.  Long SB, Campbell EB, MacKinnon R. Voltage sensor of Kv1.2: Structural basis of electromechanical coupling. Science. 2005; 309: 903-908.

57.  Holland IB, Cole SPC, Kuchler K, Higgins CF, eds. ABC Proteins: From Bacteria to Man. Amsterdam: Academic Press; 2003.

58.  Reyes CL, Ward A, Yu J, Chang G. The structures of MsbA: Insight into ABC transporter-mediated multidrug efflux. FEBS Lett. 2006; 580: 1042-1048.

59.  Reyes CL, Chang G. Structure of the ABC transporter MsbA in complex with ADP-vanadate and lipopolysaccharide. Science. 2005; 308: 1028-1031.

60.  Chang G. Structure of MsbA from Vibrio cholera: A multidrug resistance ABC transporter homolog in a closed conformation. J. Mol. Bio. 2003; 330: 419-430.

61.  Chang G, Roth CB. Structure of MsbA from E-coli: A homolog of the multidrug resistance ATP binding cassette (ABC) transporters. Science. 2001; 293: 1793-1800.

62.  Locher KP, Lee AT, Rees DC. The E-coli BtuCD structure: A framework for ABC transporter architecture and mechanism. Science. 2002; 296: 1091-1098.

63.  Borths EL, Locher KP, Lee AT, Rees DC. The structure of Escherichia coli BtuF and binding to its cognate ATP binding cassette transporter. Proc. Natl. Acad.S Sci. 2002; 99: 16642-16647.

64.  Karpowich NK, Huang HH, Smith PC, Hunt JF. Crystal structures of the BtuF periplasmic-binding protein for vitamin B12 suggest a functionally important reduction in protein mobility upon ligand binding. J. Biol. Chem. 2003; 278: 8429-8434.

65.  Stockner T, Vogel HJ, Tieleman DP. A salt-bridge motif involved in ligand binding and large-scale domain motions of the maltose-binding protein. Biophys. J. 2005; 89: 3362-3371.

66.  Davidson AL, Chen J. ATP-binding cassette transporters in bacteria. Annu. Rev. Biochem. 2004; 73: 241-268.

67.  Chen J, Lu G, Lin J, Davidson AL, Quiocho FA. A tweezers-like motion of the ATP-binding cassette dimer in an ABC transport cycle. Mol. Cell. 2003; 12: 651-661.

68.  Tieleman DP, Berendsen HJ. A molecular dynamics study of the pores formed by Escherichia coli OmpF porin in a fully hydrated palmitoyloleoylphosphatidylcholine bilayer. Biophys J. 1998; 74: 2786-2801.

69.  Lindahl E, Hess B, van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 2001; 7: 306-317.