


|
Contents

|
1. This is a concise review of the field of ion pumping from the perspective of the authors.
2. The period covered spans the discovery of Na+ and K+ concentration gradients across animal cell membranes by Carl Schmidt in the 1850s, through the isolation of the Na+,K+-ATPase by Skou in 1957 (for which he was awarded the 1997 Nobel Prize in Chemistry), to the publication of the first crystal structure of the enzyme in 2007 and beyond.
3. Contributions of the authors’ research group to the resolution of the questions of the mechanism of the allosteric role of ATP within the Na+,K+-ATPase reaction cycle and how protomeric versus diprotomeric states of the enzyme influence its kinetics are discussed within the context of the research field.
4. The results obtained indicate that the Na+,K+-ATPase has a single ATP binding site, which can be catalytic or allosteric in different parts of the enzyme’s reaction cycle.
5. The long-running controversy over whether P-type ATPases function as protomers or diprotomers can be resolved in the case of the Na+,K+-ATPase by an ATP-induced dissociation of (αβ)2 diprotomers into separate αβ protomers.
5. Kinetic data suggest that protein-protein interactions between the two αβ protomers within an (αβ)2 diprotomer result in a much lower enzymatic turnover, i.e., a lower gear, when only one of the α subunits of the diprotomer has bound ATP. The inactive αβ protomer within the diprotomer can be thought of as causing a drag on the active protomer.
Professor Alex Hope1,2 was one of the founders of the Australian Society of Biophysics. The topic of this paper, based on the inaugural McAulay-Hope Lecture, is devoted to one of his main research interests: active transport, i.e. the energy-dependent transfer of ions and molecules across the membranes of living organisms. In his own research Professor Hope concentrated on the active transport processes of plant cells, whereas we shall concentrate here on animal cells, but the fundamental principles of active transport are the same regardless of the type of organism.
The aim of the paper is to provide an overview of the field of active transport, in particular ion pumping, from the personal perspective of the authors. We hope to give some insight into how the field has developed over the years to its present state of knowledge and to describe how, in our view, some of our own contributions to the field fit within the grand scheme of things.
Until recently, progress in resolving the mechanisms of ion pumps has been a long slow process, with many hurdles and setbacks along the way. If one wishes to trace the origins of the field, it is necessary to go back to the mid-19th century.
Ion pumps are now recognized to be responsible, at least in part, for markedly different ion concentrations inside and outside of living cells. In particular, the Na+ concentration in the cytoplasm of cells is low, whereas that in the extracellular medium is relatively high. In the case of the K+ ion, the reverse is true (see Figure 1). This fact was first recognized by the pioneering physiological chemist Carl Schmidt in the early 1850s during investigations on the pathology of cholera,3 which was endemic in his native Russia at the time. This discovery came while Schmidt was comparing blood of cholera victims with that of healthy individuals.
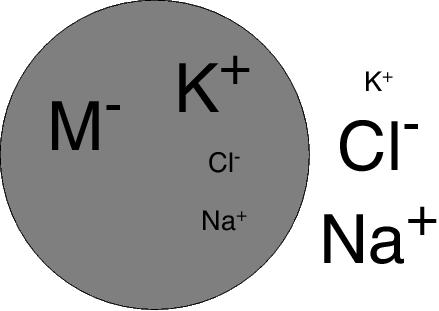
Figure 1. Ionic distributions across cell membranes. M− represents impermeant anions, e.g. negatively charged proteins. Typical intracellular (int) and extracellular (ext) con-centrations of the small inorganic ions are: [K+]int = 140-155 mM, [K+]ext = 4-5 mM, [Cl−]int = 4 mM, [Cl−]ext = 120 mM, [Na+]int = 12 mM, [Na+]ext = 145-150 mM.7,8 (Note: In the special case of red blood cells [Cl−]int is significantly higher (48-53 mM) and [Cl−]ext is lower (98-109 mM) due to exchange with HCO3− across the plasma membrane,9 which is important for CO2 excretion and the maintenance of blood pH. This exchange is known as the “chloride shift”.)
During the course of the second half of the 19th century it became clear that the ionic concentrations of all animal cells were significantly different from those of the extracellular fluids and that the secretion and absorption of ions or nutrients often involved their movement against a concentration gradient, thus requiring a source of energy. A minority of physiologists at the time still attributed this to the presence of a vital force within all living organisms, even though a decisive nail in the coffin of vitalism within chemistry was already delivered by Friedrich Wöhler,4 one of Carl Schmidt’s doctoral advisors (the other was Justus von Liebig), in 1828 when he showed that urea, an organic compound, could be synthesized from inorganic starting materials. By the end of the 19th century, however, many physiologists were attempting instead to understand membrane transport purely in terms of the physical processes of filtration and diffusion. In the 1890s, major work rejecting the involvement of a vital force as the source of energy for the transport across cell membranes and at the same time accepting the inadequacy of filtration and diffusion, was carried out by both Rudolf Heidenhain5 (University of Breslau) and Ernest Overton6 (then at the University of Zürich).
Heidenhain (doctoral advisor of Ivan Pavlov of salivating dog fame) concluded that, if filtration and diffusion cannot completely explain membrane transport, whereby in both cases the driving force lies outside of the cell membrane, i.e. due to differences in hydrostatic pressure on each side of the membrane in the case of filtration, and differences in chemical composition in the case of diffusion, then the driving force should lie within the membrane itself. As an analogy he used the idea of a “microscopic steamship” travelling against a current. Later in his paper Heidenhain even used the term “pump”, which we use today.
Overton was aware of Heidenhain’s work and came to similar conclusions. For example, he was convinced that the uptake of NaCl from the gut into the bloodstream could not be due to a pure osmotic process and must instead require energy, because otherwise one would expect the NaCl to flow in the opposite direction. He considered that the epithelial cells of the gut must be gaining the necessary energy for the NaCl uptake from metabolic processes within the cytoplasm of the cells. He termed this an “adenoid”, i.e. gland-like, activity of the cells. Although we do not use this term today, Overton was describing, quite precisely, active transport.
As in the case of Heidenhain, Overton made it very clear that he was not proposing any return to vitalism. He saw the energy necessary for the active transport of Na+ as coming directly from so-called “physiological combustion” of an animal’s food intake. Thus, the transport could continue throughout the animal’s lifetime, i.e. as long as its metabolism of nutrients continued. There was no need to assume any vital force. It is interesting here to consider Overton’s family background. In fact he was a distant relative on his mother’s side of Charles Darwin and he moved with his family due to a chronic illness of his mother to Switzerland, where he started to study botany at the University of Zürich in 1884.10 Perhaps his relation to Darwin may have partly influenced him in his total rejection of vitalism.
In 1901 Overton moved to the University of Würzburg in Germany, where he carried out further relevant work on the topic of active transport.11 There he began investigating muscle contraction. In what he considered at the time to be surprising results, he found that the presence of Na+ ions in the solution bathing a muscle fibre was necessary for muscle contraction and could not be replaced by an isoosmotic sugar solution. Based on these findings, he correctly attributed an exchange of Na+ and K+ ions across the muscle membrane as the origin of a change in electrical voltage leading to muscle contraction; an amazing achievement for the time. Furthermore, he realised a problem associated with this hypothesis, i.e., that the Na+ and K+ concentrations across the muscle membrane never equalize during an animal’s entire lifespan. Thus he concluded that there must be a “mechanism” which works against the equalization of the concentrations. We now know that this mechanism is in fact the Na+,K+-ATPase or sodium-potassium pump.
Unfortunately Overton’s hypothesis of Na+ and K+ exchange across the membrane as the origin of muscle excitability was either not widely accepted at the time or even totally dismissed. It took 50 years before the hypothesis was re-discovered and verified by the work of Hodgkin and Huxley,12 for which they both received the Nobel Prize in Medicine or Physiology in 1963. According to Kleinzeller,10 Andrew Huxley once commented that, “If people had listened to what Overton had to say about excitability, the work of Alan (Hodgkin) and myself would have been obsolete.” This raises an interesting philosophical question. What value are scientific discoveries if they are not passed on to future generations for the benefit of society? If a discovery needs to be re-discovered, it would seem that the initial discovery can be regarded as worthless or at most in hindsight of pure academic interest.
It seems that Overton was not able to convince a sufficient number of his contemporaries of the value of his Na+/K+ exchange hypothesis to ensure its survival. The reason for this may lie in part in his character and his approach to scientific research. Throughout his scientific career Overton only had one collaborator with whom he published two papers and he had no student collaborators.10 He seems to have preferred generating data with his own hands and what he did publish, he published mostly alone. Therefore, he never accumulated around him a group of disciples who could spread the “good word” of his discoveries and hypotheses. It is clear that Overton is now recognized as a pioneer of membrane physiology and some of his ideas (e.g. the pharmacology of narcotic action) were accepted in his own lifetime, but his impact on the field could have been much greater had he had the ability to sufficiently publicise his work. This stresses the imperative task of every scientist to publicise and promote their ideas if they want them to survive, rather than be forgotten and gather dust on library shelves.
In the history of science, the beginnings of quantum theory and discoveries on the structure of the atom appear to overshadow other scientific achievements of the late 19th and early 20th century. At the time, however, diffusion was another hot topic of research occupying many top physicists and physical chemists. For example, in 1901 Jacobus Henricus van’t Hoff received the first Nobel Prize in Chemistry, in part for his development of a quantitative theory of osmotic pressure. Van’t Hoff, together with another Nobel prizewinner Wilhelm Ostwald (a former doctoral student of Carl Schmidt) are generally considered, at least in the German-speaking world, to be the founders of the discipline of physical chemistry due their establishment of the Zeitschrift für physikalische Chemie in Leipzig in 1887. Another major development in the theory of diffusion in this period was Einstein’s discovery in 1905 of the link between diffusion and random Brownian motion, one of the four major discoveries of his annus mirabilis; the others being his explanation of the photoelectric effect (for which he was awarded the 1921 Nobel Prize in Physics), the special theory of relativity and the equivalence of mass and energy (E = mc2). In 1888 Walther Nernst had already developed the theory of equilibrium diffusion potentials, and in 1890 Max Planck provided a theory of electrodiffusion, summarized by what is now known as the Nernst-Planck equation. In 1917 the Polish physicist Smoluchowski published his theory of the rate of diffusion-controlled chemical reactions in solution. In terms of the topic of this paper, however, the most relevant work on diffusion published in that period is that by the Irish physical chemist Frederick Donnan on the effect of non-dialysable salts,13 which we will describe in more detail below. In the light of all of these achievements in understanding diffusion, it is natural, therefore, that physiologists of the period would attempt to explain membrane transport in terms of the newly developed theories, rather than to adopt Overton’s and Heidenhain’s idea of active transport. Another factor against the idea of active transport was its apparent wastefulness of a cell’s energy resources.
Since the time of Thomas Graham’s work on gas diffusion, dialysis and colloids in the first half of the 19th century, Britain had lost the lead in physicochemical research to mainland Europe, in particular Germany. It was, therefore, logical that, following his undergraduate degree in Ireland, Donnan should travel to the geographical focus of his research interests at the time. He carried out his PhD studies under the supervision of Ostwald at the University of Leipzig, and, after graduating in 1896, he spent some time working with van’t Hoff in Berlin. He was greatly influenced by these pioneers of physical chemistry, and, in the years following his return to Britain, the experience he had gained in Germany helped him to strengthen the discipline in the British Isles. For the topic of ion pumping the most relevant paper he published was in 1911 while he was Professor of Physical Chemistry at the University of Liverpool.13 In this paper Donnan suggested that if the cytoplasm of cells contained electrolytically dissociated non-dialysable salts, e.g. protein anions, which they do, small permeable ions would partition themselves across the membrane so as to maintain electroneutrality in both the cytoplasm and the extracellular medium. Thus, the cytoplasm would naturally tend to attract small cations, whereas the extracellular medium would accumulate anions. Referring back to Figure 1, one can see that this idea clearly makes sense for the distribution of K+ and Cl- ions across a cell membrane. Donnan’s theory, therefore, quickly gained wide acceptance. The problem is, however, that the so-called Donnan equilibrium does not explain the distribution of the Na+ ions. Based on Donnan’s theory all permeable ions of the same charge should adopt the same distribution across a membrane, but clearly the distributions of Na+ and K+ are the opposite of one another, which had been known since the days of Carl Schmidt.3 To reconcile this inconsistency, many physiologists felt forced to assume that, whereas cell membranes were permeable to K+ and Cl- ions, they should be completely impermeable to Na+ ions. The Na+ concentration gradient across the membrane they concluded must have originated at the earliest stages of cell division and persisted throughout an animal’s lifespan. This view, popular for many years, is epitomised by the work of the Irish biochemists, Boyle and Conway, published as late as 194114 following an initial outline in Nature two years earlier.15
At the time that Boyle and Conway were writing their paper, evidence already existed indicating the untenability of the notion of an impermeant sodium ion. In his paper from 1899,6 for example, Overton based his hypothesis of an active transport of sodium ions in part on results published in 1856 by the German high school teacher Wilibald Schmidt,16 who demonstrated that dead animal membranes were easily permeable to Na+ ions. Overton concluded that, if the membranes themselves were intrinsically permeable to Na+, the Na+ concentration gradient across living membranes must be maintained during the life of an animal by the active expenditure of energy. Contemporaries of Boyle and Conway were also obtaining results indicating clearly that living membranes are permeable to Na+ ions. By 1940 Wallace Fenn and his collaborator Doris Cobb17 at the University of Rochester, USA, had firmly established an exchange between Na+ and K+ occurring on stimulation of muscle, as suggested by Overton over 30 years earlier.11 In this period, radioisotopes started to become available for research, which greatly increased the accuracy of ion transport measurements. Leon Heppel, a medical student working part-time in Fenn’s laboratory used radioactive 24Na+ injected into the muscle of rats to show18 that both extracellular and intracellular Na+ could rapidly exchange with Na+ in the blood plasma of the animals. Shortly afterwards, Steinbach at Columbia University, USA, followed up on Heppel’s experiments and demonstrated19 a reversible exchange between Na+ and K+ in isolated muscle fibres. Prompted by the results of Fenn, Heppel and Steinbach, Robert Dean (also from the Department of Physiology of the University of Rochester where Fenn and Heppel were located) published20 a detailed criticism of the Donnan-equilibrium-based theory of Boyle and Conway. The logic which he used was identical to that used by Overton in 1902. Quoting directly from Dean’s paper: “It is difficult to see how the muscle can get rid of the sodium by any equilibrium process since the activity of potassium must increase in the fiber and the activity of sodium must increase in the plasma during recovery. Therefore, there must be some sort of pump, possibly located in the fiber membrane, which can pump out the sodium or, what is equivalent, pump in the potassium.”
Dean’s criticism of Boyle and Conway does not, however, mean that the theory of Donnan is incorrect. Certainly the Donnan effect is real and it needs to be either taken into account or effectively suppressed (i.e. by adding excess inert electrolyte) in equilibrium dialysis experiments. The point is that the Donnan effect cannot completely explain ion distributions across cell membranes. The Na+ and K+ ion distributions are in fact not in equilibrium even under the so-called “resting conditions” of excitable cells such as nerve or muscle, but instead in a steady-state maintained by the sodium-potassium pump. Hence the Donnan theory, as a pure equilibrium theory, can never totally explain the ion distributions. Any chemical or biological system will eventually reach equilibrium, but for any living system equilibrium equates to death.
In parallel to the work of Dean and his colleagues on muscle, a different route, but equally convincing one, to the idea of a sodium pump was being followed by researchers working on blood. In the late 1930s and early 1940s blood banks and techniques of blood transfusions were being developed in the USA, just in time for the Second World War. A practical concern in those days was the cold-storage of blood. In 1940 Solomon, Hald and Peters at Yale University, USA, found21 that when blood was transferred from 37°C to 7°C sodium and potassium seemed to cross the cell membrane in opposite directions in nearly equal amounts, clearly in contradiction to the idea of an impermeant Na+ ion. Further experiments by Danowski in the same laboratory showed22 that when the supply of glucose and hence metabolic energy was exhausted potassium flowed out of the cells in exchange for sodium at room temperature. Similar experiments were being conducted by John Harris23 at the same time at the State University of Iowa. In addition, Harris showed that the loss of K+ from cold-stored blood followed first order kinetics directly from the time of cooling without any lag, indicating that it could not be due to any cold-induced deterioration of the cells with time. Summarizing his results Harris stated: “Plainly, the view that the erythrocyte membrane is impermeable to cations, the distribution of these ions being a static phenomenon, must be abandoned. In its place must be substituted a concept of normal membrane permeability to sodium and potassium, their concentrations in the cells being maintained by one or more metabolic functions of the cells.” This corresponds precisely to the views expressed by Dean based on muscle, except that Harris did not use the word “pump”.
Dean’s proposal of a membrane-bound ion pump was not in fact entirely new. The same conclusion would be reached by reading the papers of Heidenhain5 and Overton,6,11 published at the turn of the 19th century. However, the renewal of the idea of active transport following the work of Fenn, Heppel, Steinbach, Peters, Danowski, Harris, and Dean did motivate a new generation of scientists to go in search of the sodium pump. As described by Robinson,24 acceptance of the need for a pump was not immediate, but because of the weight of support for it, there was no way it was going to disappear again from the scientific radar as it did in Overton’s day. By the middle of the century active transport of Na+ was an established fact for both muscle and red blood cells,25 i.e. for both an excitable and a non-excitable cell type.
To fulfil the criteria for identification as the sodium pump it was then clear that an enzyme should be membrane-bound, require Na+ and K+ for its activity and utilize a source of energy. However, before the sodium pump could be discovered, or more precisely, before scientists could be in a position to realize that an enzyme they had stumbled across was actually the sodium pump, further information was required. Firstly, what could the energy source be? Shortly before the publication of Dean’s critical review, the Russian scientist Vladimir Engelhardt and his PhD student (who was also his wife), Militsa Lyubimowa, discovered26 in 1939 that hydrolysis of ATP provided the energy for muscle contraction, i.e. that myosin was in fact an ATPase. That the coupling of biochemical reactions to the transfer of high energy phosphate bonds, particularly that from ATP, is a ubiquitous mechanism for driving otherwise non-spontaneous reactions was soon recognized. Solid reviews by both Fritz Lipmann27 and Hermann Kalckar28 in 1941 contributed to the quick acceptance of this realisation. Already in the 1940s, it thus appeared likely that the sodium pump should be a membrane-bound ATPase. That the uptake of potassium ions in red blood cells did in fact require ATP was confirmed in 1954 by Gárdos29 through direct experimental measurements, in which he introduced ATP into red blood cells and showed that they could continue to accumulate K+ ions even in the absence of glycolysis as long as Mg2+ ions were present as a cofactor for the ATP.
A final crucial discovery leading up to the actual isolation of the sodium pump was the finding by Schatzmann30 in 1953 that sodium and potassium transport in red blood cells could be specifically inhibited by heart glycosides, e.g. digitoxin. Since Schatzmann could show that the heart glycosides had no influence on the glycolysis of the cells, he was able to conclude that they are direct inhibitors of the sodium-potassium pump.
By the mid 1950s it was clear, therefore, that apart from being membrane-bound and requiring Na+ and K+ for its activity, the sodium-potassium pump should require ATP as an energy source and Mg2+ as a cofactor and it should be inhibitable by heart glycosides. Then in 1957 such an enzyme was isolated by Jens Christian Skou31 (University of Aarhus, Denmark) from crab nerve. In fact Skou’s discovery was serendipitous, because he was simply looking for an enzyme on which to test the action of local anaesthetics. Initially he was too cautious in the title of his paper on the topic to identify the enzyme he had discovered as the source of active transport of sodium and potassium. In the following year, however, Skou met the American physiologist Robert Post,32 soon to be a pioneer in sodium-potassium pump research in red blood cells, at a biochemistry congress in Vienna. Post asked Skou33 whether his enzyme was inhibited by ouabain, a heart glycoside. Skou was not aware of Schatzmann’s work30 and did not know what ouabain was. On returning to Aarhus, however, Skou conducted the crucial experiment and found that his enzyme was in fact inhibited by ouabain. In publishing the results of this experiment Skou then clearly suggested34 a link between his isolated enzyme and the active transport of sodium and potassium in the title of his paper. Almost 40 years later, in 1997, when there had long been no further doubt that Skou’s Na+,K+-ATPase incorporated the complete active transport machinery for sodium and potassium ions, he received the Nobel Prize in Chemistry for his discovery.
After it had become clear that the Na+,K+-ATPase was in fact synonymous with the sodium-potassium pump, the most fundamental chemical questions were what is its structure and how does it function. Information on the complete mechanism of any chemical reaction can only be determined by kinetic measurements. In the early days following the isolation of the Na+,K+-ATPase by Skou, much valuable mechanistic information was obtained by steady-state measurements of the enzyme’s activity. This led to the widely-accepted Albers-Post or E1-E2 cycle,35-37 describing the sequence of reaction steps the enzyme undergoes in transporting Na+ and K+ ions (see Figure 2). However, to determine the detailed mechanism of complex multi-step mechanisms, as involved in ion pumps, requires one to be able to resolve the kinetics of individual reaction steps. Because they undergo relatively large conformational changes as part of their reaction cycles, ion pumps have relatively low turnover numbers. The turnover of the Na+,K+-ATPase is approximately 200 s-1 at 37°C.38 This is far below the measurable ion flux through a single protein channel of around 5 × 106 s-1 (equivalent to 1 pA) using the patch-clamp technique, developed39 by Neher and Sakmann in 1976 (for which they received the Nobel Prize in Physiology or Medicine in 1991). Thus, electrical recording of single ion pump activity is currently impossible. In order to measure the kinetics of individual partial reactions, it is necessary to synchronise many pumps and activate them simultaneously. One means of rapid activation is via an ATP concentration jump, achieved by releasing it photochemically from an inactive precursor (“caged ATP”) triggered by a laser flash, a method introduced40 by Kaplan, Forbush and Hoffman at the Department of Physiology, Yale University School of Medicine. Unfortunately unphotolysed caged ATP can modify the observed kinetics by blocking ATP binding sites41 and this inhibition needs to be taken into account if one is to accurately determine rate constants.
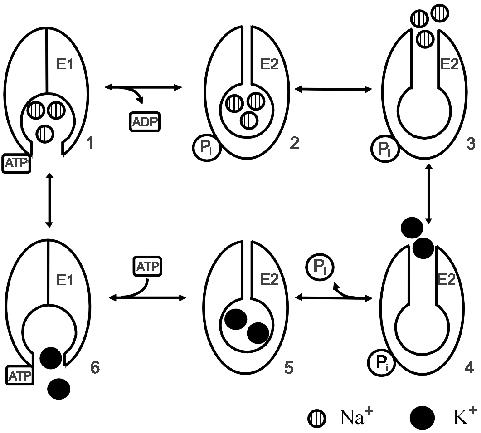
Figure 2. Albers-Post model of the mechanism of the Na+,K+-ATPase. The sequence of intermediates from 1 to 6 around the cycle correspond to the following reactions: E1(Na+)3ATP → E2P(Na+)3 → E2P → E2P(K+)2 → E2(K+)2 → E1. The diagram has been modified from Clarke (2009).44
An alternative method to simultaneously activate many pumps is to produce an ATP concentration jump by rapid mixing with ATP using the stopped-flow or quenched-flow technique. In our own research we have incorporated an electrochromic fluorescent dye into the membrane adjacent to the protein to monitor ion pump kinetics. The styrylpyridinium dye RH421, developed in the laboratory of Grinvald and Hildesheim42 at the Weizmann Institute, Israel, responds to intramembrane electric field strength changes induced by ion binding and release steps of the protein. A similar experimental approach was used by Professor Alex Hope in resolving the mechanism of the cytochrome bf complex of the photosynthetic apparatus of chloroplasts,43 except that in the case of the cytochrome bf complex the electrochromic chromophore was intrinsic to the protein, whereas the Na+,K+-ATPase has no intrinsic electrochromic chromophore and hence an extrinsic fluorophore has to be added to make the approach feasible.
An interesting question, which stopped-flow measurements using RH421 have helped answer, is the allosteric role that ATP plays in the Na+,K+-ATPase mechanism. Of course ATP provides the energy to drive Na+ and K+ transport, and it does this by transferring a phosphate group to the enzyme, forming high-energy intermediate states. However, ATP also plays an important allosteric role in accelerating the E2 → E1 conformational transition of unphosphorylated enzyme, which involves the release of K+ ions to the cytoplasm, and helping to drive the enzyme in the forward physiological ion pumping direction. This was first recognised by Post and co-workers36,37 in the early 1970s. For many years after this initial discovery, however, it remained a controversial question as to whether the enzyme had two ATP binding sites, i.e. one catalytic phosphorylating site and one allosteric site, or whether it had a single ATP site, which could alternate between catalytic and allosteric roles as the enzyme proceeded around its reaction cycle.
In 1982, Askari and Huang45 provided kinetic evidence indicating that ATP can bind to the Na+,K+-ATPase prior to dephosphorylation, i.e. ATP and Pi can be bound to the enzyme simultaneously. This would certainly exclude the possibility of a single ATP binding site fulfilling both catalytic and allosteric roles, if the ATP binding site and the phosphorylation site were not sufficiently spatially separated. However, recent crystal structural data indicate that they are in fact separated. Of particular relevance here is a structure of an E2P-ATP analogue form of the sarcoplasmic reticulum Ca2+-ATPase (a P-type ATPase related to the Na+,K+-ATPase), published by Olesen et al.46 in 2007, in which the authors used AlF4− as an analogue of inorganic phosphate and the non-hydrolysable ATP derivative AMPPCP. This structure shows that P-type ATPases possess separate ATP binding and phosphorylation sites, and that phosphorylation does not preclude ATP binding. Hence there is no reason why an allosterically bound ATP could not function catalytically at a later point in the cycle on a single ion pump molecule. Stopped-flow measurements utilizing RH421 showed47 conclusively that this in fact occurs for the Na+,K+-ATPase.
By rapidly mixing the enzyme in the absence of Mg2+ ions simultaneously with NaCl and ATP, a perturbation of the E2 ↔ E1 equilibrium of unphosphorylated enzyme could be induced through the formation of the E1(Na+)3 state. The ATP concentration dependence of the rate of relaxation of the E2 ↔ E1 equilibrium showed an acceleration occurring in two stages.47 In the submicromolar ATP concentration range (typical of catalytic ATP binding to the E1 state) an acceleration of the reverse reaction, E1 → E2, was observed, indicating that catalytic ATP binding, which can stimulate phosphorylation in the presence of Mg2+ ions, simultaneously has an allosteric effect on a conformational transition of the enzyme. At higher ATP concentrations, in the range of hundreds of micromolar (typical of allosteric ATP binding to the E2 state), a second phase of ATP acceleration of the relaxation of the E2 ↔ E1 equilibrium was observed, indicating acceleration of the forward reaction, E2 → E1. Therefore, the results showed that the same ATP binding site can be catalytic or allosteric depending on which part of the reaction cycle one is considering. There is no need for the enzyme to possess separate catalytic and allosteric ATP binding sites.
In fact, then, the use of the adjective “allosteric” for the effect of ATP on the E2/E1 conformational transition of the Na+,K+-ATPase does not conform with the original definition of the word when it was first introduced by Monod, Changeux and Jacob48,49 in the early 1960s. The etymology of the word is that it derives from the Greek αλλορ (allos), meaning “other”, which Monod, Changeux and Jacob specifically chose to imply an interaction of a small molecular species with a site distinct from, or not overlapping with, the active site. Therefore, the question arises as to whether ATP should be described as an “allosteric” effector of the Na+,K+-ATPase at all. Since Monod, Changeux and Jacob’s early work, however, a number of cases of substrate-like effectors binding to the active site of allosteric enzymes have been identified.50 Hence, it seems unreasonable to exclude active-site interaction as a possible mechanism within the definition of an allosteric effector. A wider definition of the word “allosteric”, ignoring its original etymology, would seem to be appropriate. Kuriyan and Eisenberg51 suggested the definition of allostery as regulation of a protein through a change in its tertiary structure, quaternary structure or its flexibility by a small molecule or other protein. Within this broader definition ATP can still be classed an allosteric effector of the Na+,K+-ATPase.
The Na+,K+-ATPase consists of a major catalytic α-subunit, a smaller β-subunit and an even smaller γ-subunit or FXYD protein. One of the most fiercely debated questions of the ion pump field over the last 40 years has been the composition of the functional unit of the enzyme, i.e. (ignoring the γ-subunit) does the enzyme function as an (αβ) protomer or an (αβ)2 diprotomer? That the Na+,K+-ATPase might function as a diprotomer was first suggested by Stein et al.52 and Repke and Schön53 in 1973. From that time on, many arguments for and against diprotomers or higher oligomers have been presented.44 Since the beginning of the 21st century, when the publication of the first crystal structures of P-type ATPases started to appear,46,54-56 it has become clear that dimerisation is not necessary to form an ion transport pathway. Ion transport for the Na+,K+-ATPase, for example, occurs through the centre of the α-subunit. This does not necessarily mean, however, that in a native cell membrane the protein does not aggregate into diprotomers or higher oligomers, or that oligomerisation has no physiological role to play.
The occurrence of heated discussions at ion pump meetings over whether the Na+,K+-ATPase exists as a protomer or a diprotomer proves how passionately certain individuals favour one view or the other. In fact, perhaps the truth lies somewhere between. The proportion of arrogant people within the scientific community who believe that they possess the whole truth is probably just as high as within society in general. But, in the authors’ experience, scientists are also not stupid. If a large enough number of scientists argue in favour of either monomers or dimers, then there would seem to be a high likelihood that both groups are in possession of some of the truth. In this context it is worthwhile recalling the hypothesis of the great 19th century German philosopher Hegel concerning the process by which scientific knowledge advances. According to Hegel, the acquisition of scientific truth passes through three phases: the thesis, the antithesis and finally the synthesis (although Hegel never used these specific terms). A classic example is the nature of matter. The thesis put forward by the ancient Greek philosopher Democritus was that matter was composed of particles (atoms). Other Greek philosophers, notably Anaxagoras and Aristotle (supporters of the view that “nature abhors a vacuum”) proposed the antithesis that matter is continuous. The synthesis finally came over 2,000 years later with the proposal of the wave-particle duality of matter by Louis de Broglie in 1924.
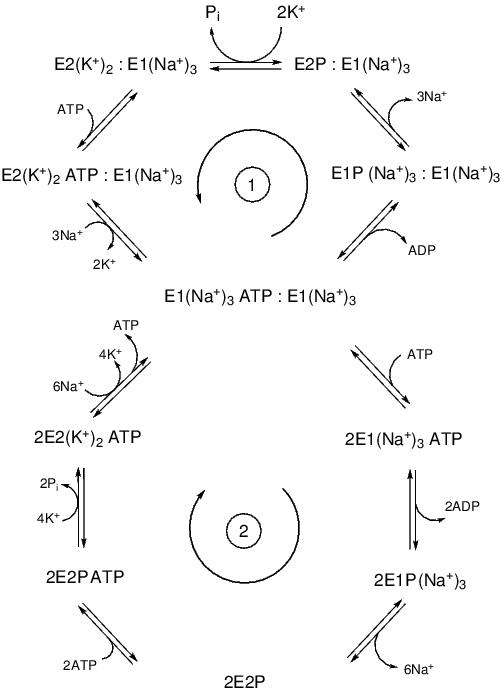
Figure 3. Two-gear dimeric model of the Na+,K+-ATPase mechanism. The upper cycle (1) represents the low-gear pathway followed at low concentrations of ATP, when only one of the ATP binding sites of an α-subunit is occupied. The lower cycle (2) represents the high-gear pathway followed at high concentrations of ATP, when both of the ATP sites of an (αβ)2 dimer are occupied and the enzyme has dissociated into two separate αβ protomers. The arrows in the centre of the cycles represent the physiological direction of cycling by the enzyme. The diagram has been modified from Clarke & Kane.57
A possible synthesis of the protomeric and diprotomeric hypotheses of the Na+,K+-ATPase structure is that the oligomeric state of the protein can vary depending on the experimental or physiological conditions. There is clear evidence from experiments in which the protein has been reconstituted into synthetic vesicles that an αβ protomer can carry out pumping of both Na+ and K+ ions.58 However, recent stopped-flow kinetic studies on Na+,K+-ATPase membrane fragments from mammalian kidney preparations have indicated that both αβ protomers and (αβ)2 diprotomers are capable of carrying out ion pumping, but with different kinetics, i.e. the enzyme possesses two gears57,59 (see Figure 3). The higher gear, with a tenfold higher rate constant for phosphorylation and conversion of the enzyme into the E2P state, occurs when the enzyme is in the monomeric αβ state, whereas the lower gear is associated with the (αβ)2 dimeric state. Measurements conducted over a wide range of ATP concentrations provided evidence that a transition from the (αβ)2 to the αβ state and a consequent shifting from the low to the high gear is induced by ATP binding to both of the α subunits within a dimer. The kinetic model shown in Figure 3 thus incorporates both the monomeric and the dimeric points of view and provides a link between the protein’s quaternary structure and its mechanism. X-ray crystal structures of the sarcoplasmic reticulum Ca2+-ATPase have shown that ATP binding causes a closing of the cytoplasmic domains into a more compact conformation.60-62 It seems likely, therefore, that the ATP-induced dissociation of (αβ)2 diprotomers into αβ protomers could be due to a reduction in contacts between the cytoplasmic domains of adjacent α-subunits within the membrane.
From the discovery of the Na+ and K+ concentration gradients across the plasma membrane of animal cells by Carl Schmidt in the 1850s, one hundred years passed before the enzyme responsible for these gradients, the Na+,K+-ATPase, was isolated.31 Another fifty years passed before the first crystal structure of the Na+,K+-ATPase was determined55 in 2007. This slow progress indicates what a complex process ion pumping is. Nevertheless, great strides forward have been made, new avenues of research are opening up and further progress can be expected.
At the molecular level the mechanism of the Na+,K+-ATPase is now well understood. With the publication of crystal structures of the Na+,K+-ATPase and other P-type ATPases since 2000, it has now become feasible to obtain a more detailed understanding of the mechanisms of the enzymes at the atomic level. Atomically resolved structures are a pre-requisite for molecular dynamic simulations of protein function. Although it is still very early days, an increasing number of theoreticians are now likely to brave the complexity of ion pumps and obtain new insights into how they work.
Even if the structures of and mechanisms of individual ion pumps are eventually fully resolved, the more medically relevant questions of how they interact with other cellular proteins and how they are regulated will remain active areas of research for many years to come. The Na+ and K+ gradients across the plasma membrane created by the Na+,K+-ATPase provide a secondary source of energy driving the activity of numerous ion channels and transporters. In this way the Na+,K+-ATPase plays a crucial role in such a diverse range of physiological processes as nutrient uptake, muscle contraction, nerve function and cell volume regulation. The heat that it produces as a by-product of ATP hydrolysis is even thought to be a major determinant of body temperature. In studies of all of these physiological processes and the pathological conditions associated with them (e.g. cardiovascular disease, diabetes, epilepsy, high blood pressure) the information gained over the last 150 years and particularly the last 50 years on the structure and mechanism of the Na+,K+-ATPase will provide a solid foundation on which to build.
RJC dedicates this paper to his mother, the late Mrs. Vera Clarke. He would like to thank the late Prof. Peter Läuger who introduced him to ion pumps and who was such an invaluable mentor to him in the early stages of his career. He would also like to thank his collaborators, without whom he could not have continued to work in the field and make any worthwhile contribution. In particular he would like to thank Prof. Hans-Jürgen Apell, Prof. Ernst Bamberg, Dr. Flemming Cornelius, Prof. Paul Else, Dr. Klaus Fendler, the late Dr. Jeffrey Froehlich, Dr. Ernst Grell, Prof. Philip Kuchel, and Prof. Helge Rasmussen.
1. Barry PH, Coster HGL, Chow WS. Biographical memoir: Alexander Beaumont Hope, Australian biophysicist, 1928-2008. Eur. Biophys. J. 2009; 39: 175-8.
2. Chow WS. Alexander Beaumont Hope (1928-2008): an Australian biophysicist. Photosynth. Res. 2010; 105: 83-8.
3. Zaleski SS. Carl Schmidt. Chem. Ber. 1894; 27: 963-78.
4. Wöhler F. Ueber künstliche Bildung des Harnstoffs. Ann. Phys. Chem. 1828; 88: 253-6.
5. Heidenhain R. Neue Versuche über die Aufsaugung im Dünndarm. Pflügers Archiv 1894; 56: 579-631.
6. Overton E. Ueber die allgemeinen osmotischen Eigenschaften der Zelle, ihre vermutlichen Ursachen und ihre Bedeutung für die Physiologie. Vierteljahrsschr. Naturforsch. Ges. Zürich 1899; 44: 88-135.
7. Darnell J, Lodish H, Baltimore D. Molecular Cell Biology, 2nd edition. Scientific American Books, New York. 1990; 772.
8. Dudel J. Fundamentals of Cell Physiology. In: Schmidt RF, Thews G (eds.). Human Physiology, 2nd edition. Springer, Berlin. 1989; 4.
9. Raftos JE, Bulliman BT, Kuchel PW. Evaluation of an electrochemical model of erythrocyte pH buffering using 31P nuclear magnetic resonance data. J. Gen. Physiol. 1990; 95: 1183-1204.
10. Kleinzeller A. Ernest Overton’s contribution to the cell membrane concept: A centennial appreciation. News Physiol. Sci. 1997; 12: 49-53.
11. Overton E. Beiträge zur allgemeinen Muskel- und Nervenphysilogie. II. Ueber die Unentbehrlichkeit von Natrium- (oder Lithium-)Ionen für den Contractionsact des Muskels. Pflügers Archiv 1902; 92: 346-86.
12. Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952; 117: 500-44.
13. Donnan FG. Theorie der Membrangleichgewichte und Membranpotentiale bei Vorhandensein von nicht dialysierenden Elektrolyten. Ein Beitrag zur physikalisch-chemischen Physiologie. Z. Elektrochem. Angew. Phys. Chem. 1911; 17: 572-81.
14. Boyle PJ, Conway EJ. Potassium accumulation in muscle and associated changes. J. Physiol. 1941; 100: 1-63.
15. Conway EJ, Boyle PJ. A mechanism for the concentrating of potassium by cells, with experimental verification for muscle. Nature 1939; 144: 709-10.
16. Schmidt W. Versuche über Filtrationsgeschwindigkeit verschiedener Flüssigkeiten durch thierische Membran. Ann. Phys. Chem. 1856; 99: 337-88.
17. Fenn WO, Cobb DM. Electrolyte changes in muscle during activity. Am. J. Physiol. 1936; 115: 345-56.
18. Heppel LA. The diffusion of radioactive sodium into the muscles of potassium-deprived rats. Am. J. Physiol. 1940; 128: 449-54.
19. Steinbach HB. Sodium and potassium in frog muscle. J. Biol. Chem. 1940; 133: 695-701.
20. Dean RB. Theories of electrolyte equilibrium in muscle. Biol. Symp. 1941; 3: 331-48.
21. Solomon RZ, Hald PM, Peters JP. The state of the inorganic components of human red blood cells. J. Biol. Chem. 1940; 132: 723-38.
22. Danowski TS. The transfer of potassium across the human blood cell membrane. J. Biol. Chem. 1941; 139: 693-705.
23. Harris JE. The influence of the metabolism of human erythrocytes on their potassium content. J. Biol. Chem. 1941; 141: 579-95.
24. Robinson JD. Steps to the Na+-K+ pump and Na+-K+-ATPase (1939-1962). News Physiol. Sci. 1995; 10: 184-8.
25. De Weer P. A century of thinking about cell membranes. Annu. Rev. Physiol. 2000; 62: 919-26.
26. Engelhardt WW, Lyubimowa MN. Myosine and adenosinetriphosphatase. Nature 1939; 144: 668-9.
27. Lipmann F. Metabolic generation and utilization of phosphate bond energy. Adv. Enzymol. 1941; 1: 99-162.
28. Kalckar H. The nature of energetic coupling in biological syntheses. Chem. Rev. 1941; 28: 71-178.
29. Gárdos G. Akkumulation der Kaliumionen durch menschliche Blutkörperchen. Acta Physiol. Hung. 1954; 6: 191-9.
30. Schatzmann HJ. Herzglykoside als Hemmstoffe für den aktiven Kalium- und Natriumtransport durch die Erythrocytenmembran. Helv. Physiol. Acta 1953; 11: 346-54.
31. Skou JC. The influence of some cations on an adenosine triphosphatase from peripheral nerves. Biochim. Biophys. Acta 1957; 23: 394-401.
32. Post RL, Merritt CR, Kinsolving CR, Albright CD. Membrane adenosine triphosphatase as a participant in the active transport of sodium and potassium in the human erythrocyte. J. Biol. Chem. 1960; 235: 1796-1802.
33. Skou JC. The identification of the sodium pump as the membrane-bound Na+/K+-ATPase: a commentary. Biochim. Biophys. Acta 1989; 1000: 435-8.
34. Skou JC. Further investigations of Mg2+ + Na+-activated adenosinetriphosphatase, possibly related to the active, linked transport of Na+ and K+ across the nerve membrane. Biochim. Biophys. Acta 1960; 42: 6-23.
35. Albers RW. Biochemical aspects of active transport. Annu. Rev. Biochem. 1967; 36: 727-56.
36. Hegyvary C, Post RL. Binding of adenosine triphosphate to sodium and potassium ion-stimulated adenosine triphosphatase. J. Biol. Chem. 1971; 246: 5234-40.
37. Post RL, Hegyvary C, Kume S. Activation of adenosine triphosphatase in the phosphorylation kinetics of sodium and potassium ion transport adenosine triphosphatase. J. Biol. Chem. 1972; 247: 6530-40.
38. Lüpfert C, Grell E, Pintschovius V, Apell HJ, Cornelius F, Clarke RJ. Rate limitation of the Na+,K+-ATPase pump cycle. Biophys. J. 2001; 81: 2069-81.
39. Neher E, Sakmann B. Single-channel currents recorded from membrane of denervated frog muscle fibres. Nature 1976; 260: 799-802.
40. Kaplan JH, Forbush B III, Hoffman JF. Rapid photolytic release of adenosine 5′-triphosphate from a protected analogue: Utilization by the Na:K pump of human red blood cells. Biochemistry 1978; 17: 1929-35.
41. Clarke RJ, Kane DJ, Apell H-J, Roudna M, Bamberg E. Kinetics of Na+-dependent conformational changes of rabbit kidney Na+,K+-ATPase. Biophys. J. 1998; 75: 1340-53.
42. Grinvald A, Fine A, Farber IC, Hildesheim R. Fluorescence monitoring of electrical responses from small neurons and their processes. Biophys. J. 1983; 42: 195-8.
43. Hope AB. The chloroplast cytochrome bf complex: a critical focus on function. Biochim. Biophys. Acta 1993; 1143: 1-22.
44. Clarke RJ. Mechanism of allosteric effects of ATP on the kinetics of P-type ATPases. Eur. Biophys. J. 2009; 39: 3-17.
45. Askari A, Huang W. Na+,K+-ATPase: evidence for the binding of ATP to the phosphoenzyme. Biochim. Biophys. Res. Commun. 1982; 104: 1447-53.
46. Olesen C, Picard M, Winther A-ML, Gyrup C, Morth JP, Oxvig C, Møller JV, Nissen P. The structural basis of calcium transport by the calcium pump. Nature 2007; 450: 1036-44.
47. Clarke RJ, Apell H-J, Kong BY. Allosteric effect of ATP on Na+,K+-ATPase conformational kinetics. Biochemistry 2007; 46: 7034-44.
48. Monod J, Changeux J-P, Jacob F. Allosteric proteins and cellular control systems. J. Mol. Biol. 1963; 6: 306-29.
49. Changeux J-P. 50th anniversary of the word “Allosteric”. Protein Sci. 2011; 20: 1119-24.
50. Smith GD, Roberts DV, Kuchel PW. Active site directed effectors of allosteric enzymes. Biochim. Biophys. Acta 1975; 377: 197-202.
51. Kuriyan J, Eisenberg D. The origins of protein interactions and allostery in colocalization. Nature 2007; 450: 983-90.
52. Stein WD, Lieb WR, Karlish SJD, Eilam Y. A model for active transport of sodium and potassium ions as mediated by a tetrameric enzyme. Proc. Natl. Acad. Sci. USA. 1973; 70: 275-8.
53. Repke KRH, Schön R. Flip-flop model of (NaK)-ATPase function. Acta Biol. Med. Ger. 1973; 31: K19-30.
54. Toyoshima C, Nasasako M, Nomura H, Ogawa H. Crystal structure of the calcium pump of sarcoplasmic reticulum at 2.6 Å resolution. Nature 2000; 405: 647-55.
55. Morth JP, Pedersen BP, Toustrup-Jensen MS, Sørensen TL-M, Petersen J, Andersen JP, Vilsen B, Nissen P. Crystal structure of the sodium-potassium pump. Nature 2007; 450: 1043-9.
56. Shinoda T, Ogawa H, Cornelius F, Toyoshima C. Crystal structure of the sodium-potassium pump at 2.4 Å resolution. Nature 2009; 459: 446-50.
57. Clarke RJ, Kane DJ. Two gears of pumping by the sodium pump. Biophys. J. 2007; 93: 4187-96.
58. Cornelius F. Phosphorylation/dephosphorylation of reconstituted shark Na+,K+-ATPase: on phosphorylation site per αβ protomer. Biochim. Biophys. Acta 1995; 1235: 197-204.
59. Khalid M, Fouassier G, Apell HJ, Cornelius F, Clarke RJ. Interaction of ATP with the phosphoenzyme of the Na+,K+-ATPase. Biochemistry 2010; 49: 1248-58.
60. Sørensen TL-M, Møller JV, Nissen P. Phosphoryl transfer and calcium ion occlusion in the calcium pump. Science 2004; 304: 1672-5.
61. Jensen A-ML, Sørensen TL-M, Olesen C, Møller JV, Nissen P. Modulatory and catalytic modes of ATP binding by the calcium pump. EMBO J. 2006; 25: 2305-14.
62. Olesen C, Sørensen TL-M, Nielsen RC, Møller JV, Nissen P. Dephosphorylation of the calcium pump coupled to counterion occlusion. Science 2004; 306: 2251-5.